We are always looking for highly skilled and motivated applicants to join our research group as project bachelor or master students, PhD students or postdocs.
We have currently a number of PhD and postdoc openings, in particular for postdocs with ideally a strong background in AMO physics and quantum error correction – more information can be found here.
For inquiries regarding the positions, please contact Markus Müller.
B.Sc. and M.Sc. Projects
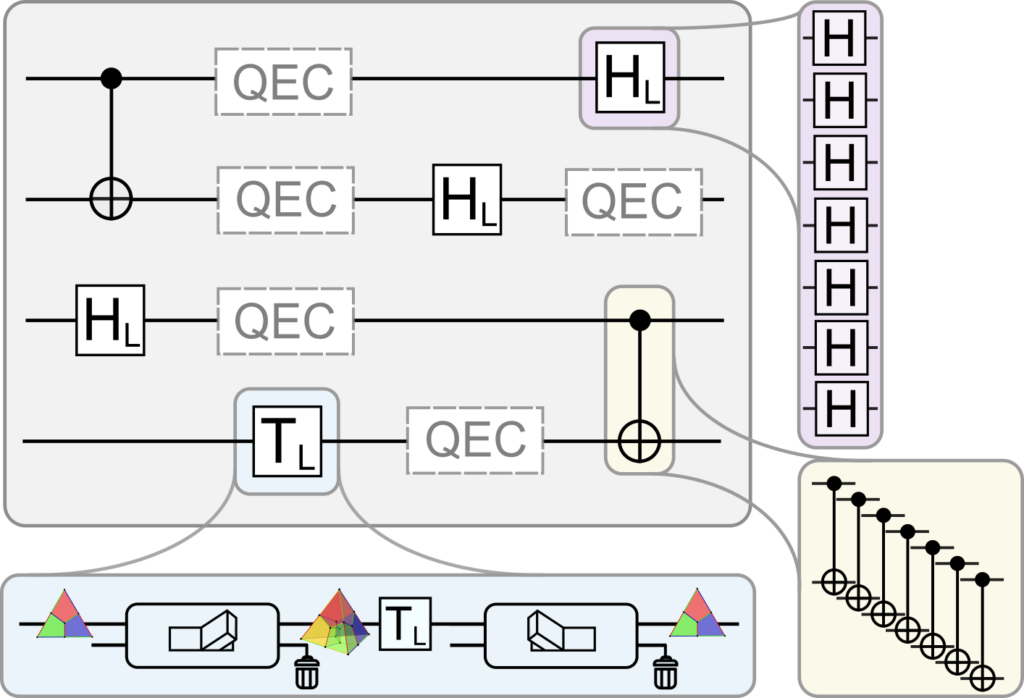
M.Sc. Project: Measurement-free algorithms for near-term quantum processors
The accuracy of quantum algorithms is limited by noise due to interactions with the environment. Traditional approaches for reliable execution of quantum algorithms make use of measurements and conditional quantum feedback based on these outcomes. However, these mid-circuit measurements are comparably slow and feed-forward operations are experimentally demanding, which limits the feasibility of quantum algorithms on current hardware. We circumvent these limitations through the design of measurement-free algorithms, where quantum computing can be run autonomously without measurement interventions through suitable circuit designs. In this project, you will extend theoretical frameworks and practical implementations [1-3] and investigate possible improvements, as well as new circuit constructions for measurement-free quantum computing.
[1]: S. Heußen et. al., PRX Quantum 5, 010333 (2024)
[2]: S. Veroni et. al., arXiv 2412.15187 (2024)
[3]: F. Butt et. al., arXiv 2410.13568 (2024)
Contact: Friederike Butt, Markus Müller
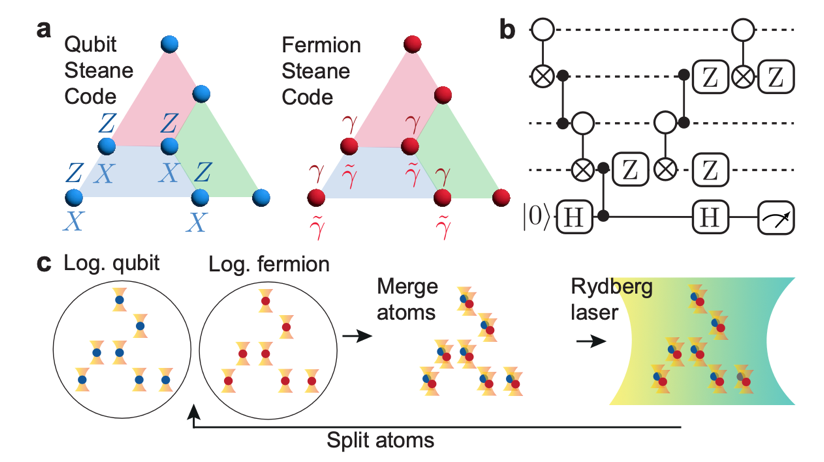
A. Schuckert et. al. arXiv 2411.08955 (2024)
B.Sc./M.Sc. Project: Fermionic fault-tolerant quantum computing
Quantum simulations of fermionic systems with qubit-based quantum computers require that fermionic exchange statistics are encoded on a software-level. This algorithmic overhead can be avoided by utilizing physical fermionic modes as computational building blocks, such as fermionic atoms trapped in optical tweezers. Executing robust quantum algorithms in such setups, however, demands the application of quantum error correction techniques.
In this project you will become acquainted with fermionic quantum computing and you will explore how quantum error correction and fault-tolerant logical gates can be performed in fermionic quantum processors. Possibly, you will study the realization of such schemes with neutral atoms in tweezer arrays.
[1] A. Schuckert et. al. arXiv 2411.08955 (2024)
[2] R. Ott et. al. arXiv 2412.16081 (2024)
[3] D. González-Cuadra et. al, PNAS 120 35 (2023)
Contact: David Locher, Luis Colmenarez, Markus Müller
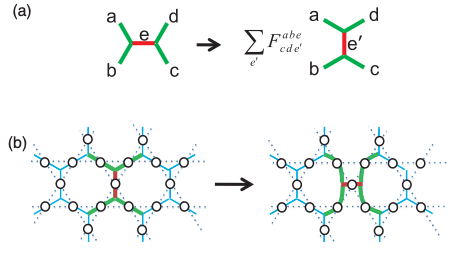
M.Sc. Project Finding the F-move gate representation for multicolor non-Abelian anyonic topological codes
Anyons are quasi-particles described by statistics that neither are bosons nor fermions. These particles emerge in certain 2D error-correction codes. The key to perform universal operations on non-Abelian anyonic codes is anyon fusion, splitting and braiding. When anyons fuse or split, they give rise to different anyons, whose fusion or splitting history is represented as a tree. These trees store robust logical information. Conversion between trees requires the application of a special unitary operation: the F move. It is known that for the Fibonacci code the F moves have a quantum circuit representation, but it remains unclear how to generalize this design to general non-Abelian anyonic models. In this project, you will first learn the basics of non-Abelian quantum computing, and then investigate non-Abelian anyonic models with the goal to design an F-move quantum circuit.
(Picture taken from: N. E. Bonesteel and D. P. DiVincenzo, Physical Review B 86, 165113 (2012).)
Contact: Thiago L. M. Guedes, Markus Müller
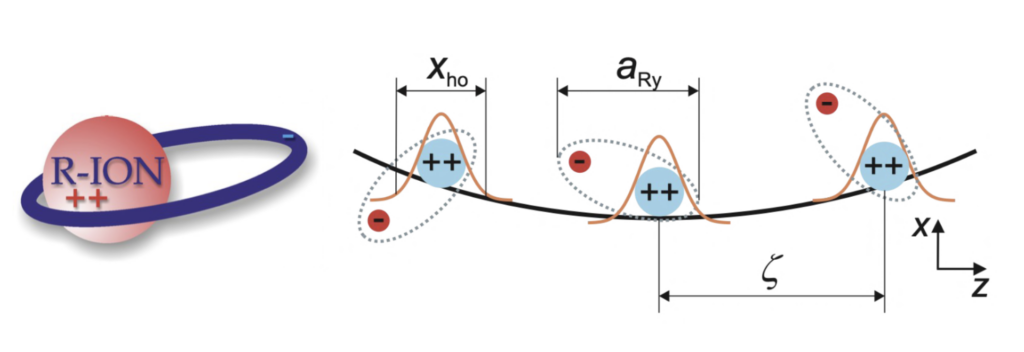
B.Sc. Project Quantum Processing with Trapped Rydberg Ions
Trapped Rydberg ions are a promising novel emerging physical platform to build quantum computers and simulators. Here, trapped ions are laser-excited to Rydberg states, where they behave as a composite object and exhibit strong and long-range interactions, which enable the realisation of fast quantum gate operations and quantum simulation of many-body spin models. In this project, you will theoretically model Rydberg ions in a Paul trap and use analytical techniques as well as numerical methods (such as Lindblad quantum master equations) to develop protocols and study the performance of quantum gate operations and building blocks for quantum error correction in this system.
Contact: Katrin Bolsmann, Markus Müller
Phys. Rev. Lett. 123, 231108 (2019)
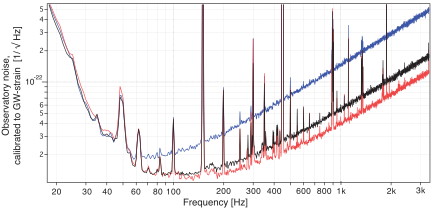
M.Sc. Project Quantum interferometry for gravitational-wave detection
Since the detection of gravitational waves at LIGO, the field of gravitational-wave detection has witnessed an unprecedent period of expansion into interdisciplinary domains. The potential of having yet another source of information about the universe has led the quantum optics and information communities to seek for quantumly enhanced (and potentially small-scale) means for gravitational-wave detection. Following this trend, we propose to study a specific design of microscopic interferometer injected with quantum states, as an alternative to the LIGO setups. We are looking for talented students with sound knowledge of quantum mechanics and either base knowledge of field theory or eagerness to learn the topic.
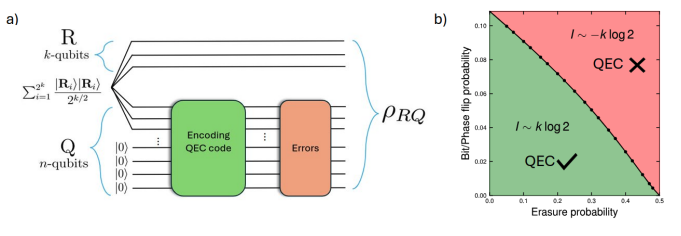
B.Sc./M.Sc. Project: Fundamental properties of topological and LDPC codes
In light of recent developments in quantum error correction (QEC) (see Ref.), particularly with the introduction of new tools such as the coherent information, we will investigate fundamental properties of QEC codes, including equivalences between families of topological and subsystem codes, as well as the extension of these tools to low-density parity check (LDPC) codes. The project involves learning, developing, and applying analytical and numerical techniques to both theoretical and practical problems of relevant QEC codes.
[1] Fan et al. PRX Quantum 5, 020343 (2024)
[2] Colmenarez, et al. Physical Review Research 6, L042014 (2024)
[3] Huang et al. arxiv:2412.12279 (2024)
[4] Colmenarez et al. arXiv:2412.16727 (2024)
Contact: Luis Colmenarez, Markus Müller
(last updated Jan 17, 2025)

